Las asíntotas de una función racional son rectas a la cual la gráfica de la función se va acercando indefinidamente pero nunca llega a tocarlas. Existen tres tipos de asíntotas: las asíntotas verticales, las asíntotas horizontales y las asíntotas oblicuas. A continuación, tienes representadas gráficamente de color rojo los tres tipos.. Las asintotas de las funciones racionales son líneas rectas horizontales, verticales u oblicuas a las que la función se aproxima a medida que la variable independiente se acerca a un valor muy grande o muy pequeño. Encontrar y comprender las asintotas de una función racional es fundamental para entender su comportamiento a largo plazo y para trazar de manera precisa su gráfica.

Dominio de una función racional Como se calcula el dominio de una función racional Ejemplos

Funciones racionales Ejemplo 1 YouTube

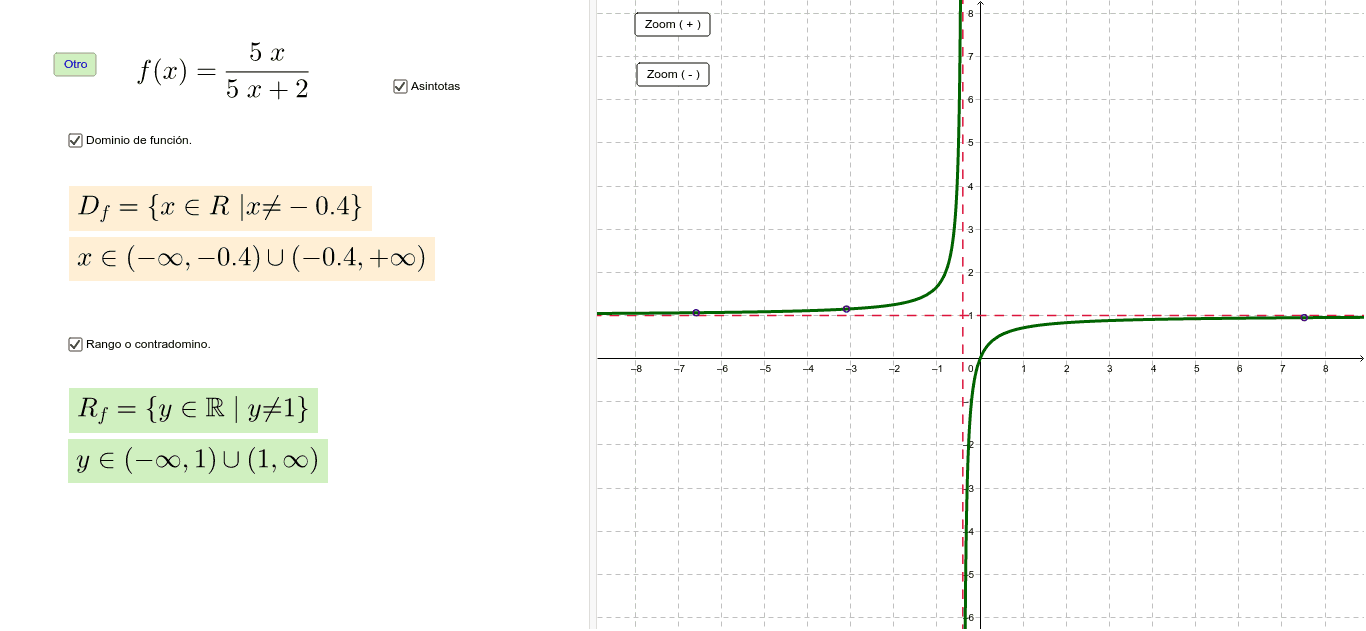
Dominio y rango de una función racional GeoGebra

USO DE GEOGEBRA PARA GRAFICAR UNA FUNCIÓN RACIONAL Y ENCONTRAR SUS ASÍNTOTAS Y DOMINIO YouTube

FUNCIÓN RACIONAL Análisis Completo Dominio, rango, ceros raíces función, intervalos de C+ y C

Asociar un gráfico con la función racional correspondiente dos asíntotas verticales YouTube

Función Racional Ejercicios Nivel 3 Aplicaciones YouTube

Función Racional Análisis Completo YouTube

FUNCION RACIONAL EJEMPLO 1f(x)=1/x YouTube

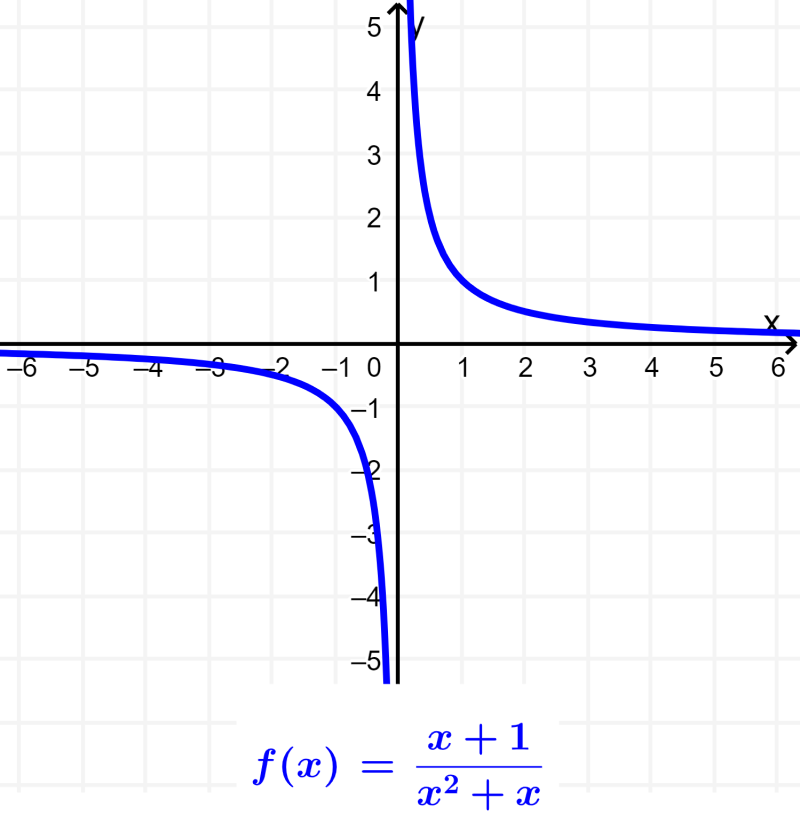
Ejercicios de Funciones Racionales Resueltos y para Resolver Neurochispas

Pendiente de una recta tangente a una funcion racional en un punto dado YouTube

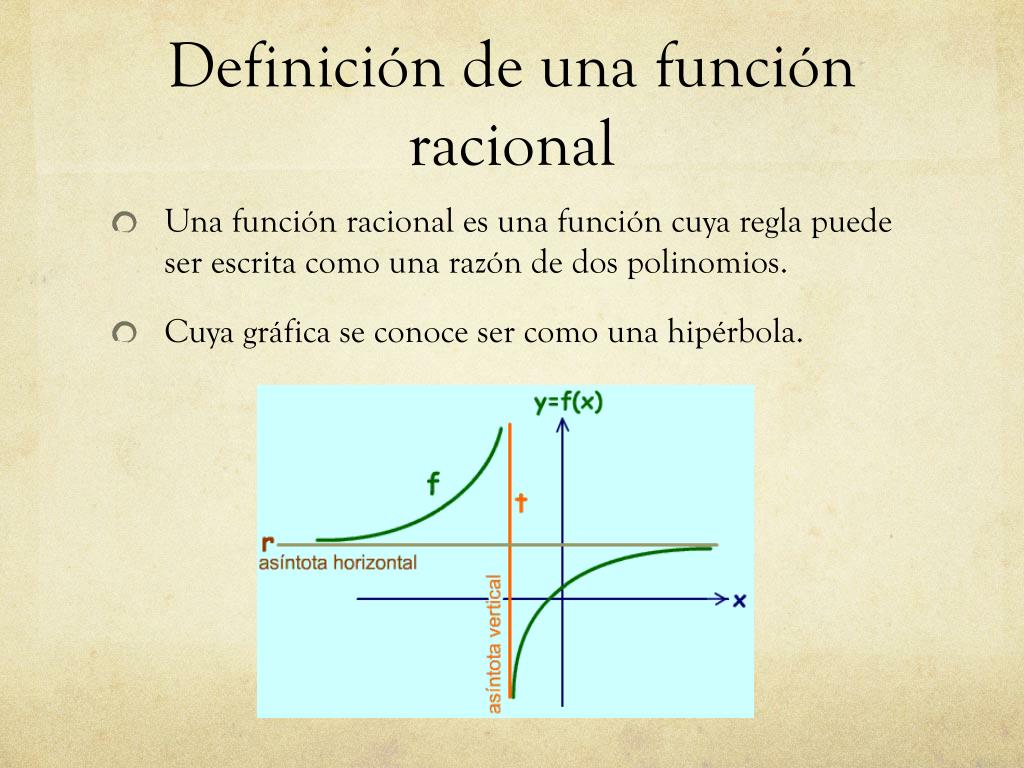
PPT Función Racional* PowerPoint Presentation, free download ID7073269

Función Racional (Análisis Completo) YouTube

Función Racional Gráfico, dominio y rango YouTube

Problema de Aplicación de la Función Racional YouTube

Función Racional YouTube

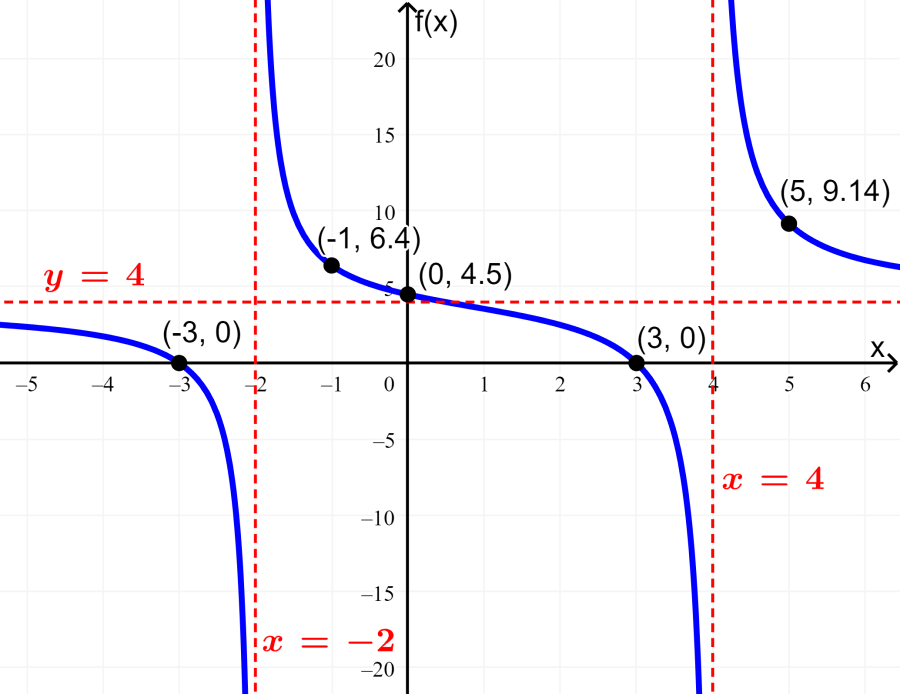
Ejercicios de Funciones Racionales Resueltos y para Resolver Neurochispas

Gráfica de funciones racionales

Dominio y rango de funciones racionales 11 ejercicios explicados paso a paso La Prof Lina M3

Ejercicios de Funciones Racionales Resueltos y para Resolver Neurochispas

7.3: Graficar funciones racionales. Hemos visto que nunca se permite que el denominador de una función racional sea igual a cero; la división por cero no está definida. Entonces, con las funciones racionales, hay valores especiales de la variable independiente que son de particular importancia. Ahora bien, no sorprende que cerca de valores.. Para graficar funciones racionales, seguimos los siguientes pasos: Paso 1: Encuentra los interceptos si es que existen. El intercepto en y es el punto (0, f (0)) y encontramos los interceptos en x al establecer al denominador como una ecuación igual a cero y resolver para x. Paso 2: Encontramos las asíntotas verticales al establecer al.